I’m going to change this story slightly because I don’t want to call out a specific person when I have seen the same thing over and over from “STEM” or “STEAM” or “STREAM” programs. Generally, the more letters they have, the bigger problem it is.
I agree with everything Ms. X says when she starts talking,
“In our district, less than half of the children graduate high school. Less than half of the graduates go on to college. Of those who attend college, the graduation rate is in the teens, usually 17-19%. Most of them drop out in the first semester. They are just not prepared for college. The area in which they are least prepared is math. So, we decided to have a STEM program for these students.
– many, many people over the years
I’m all on board with this idea, but when I look at their programs, they are something like this:
- *** Students read biographies of famous mathematicians and scientist from their ethnic/ racial group
- *** Art projects in which students build a tipi , pyramid or other structure from the history of their racial / ethnic group
Here is the problem. I teach statistics. Here is the formula for the sample standard deviation. One of the more basic statistics learned in introductory statistics in college.
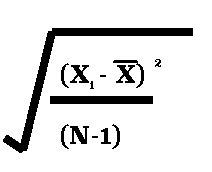
I have had students ask me:
“What does N stand for?”
“What is that 2 next to the parentheses?”
“What is that thing that looks like a weird V with a top?”
Nowhere in these “STEM” activities do students learn what an exponent is
I really, really want students to succeed in my classes. I make youtube videos of how to conduct analyses with statistical software, like this one on confidence limits for the mean and a lot more extra effort to make statistics understandable. However, if they don’t come in with some basic level of mathematics, it is going to be very difficult for them to succeed. By basic, I mean, what is a radical, what’s a square root, what’s an exponent, the difference between a variable and a constant.
Because I think the STEM / STEAM / STREAM camps and after-school activities are a good start and I don’t want to be a big jerk by pointing out problems with no solution, the next few posts are going to be examples of DIRECT TEACHING OF MATH.
Example 1: The campfire

I saw a really great activity that began with a story of one tribe stealing horses from another. The other tribe came and kidnapped some children to get even. When the kidnappers stopped to rest, the children slipped away. Since they knew their tribe was coming to rescue them, they built a campfire.
The challenge activity was to build a campfire circle no more than 18 inches in diameter using “rocks” – actually, balloons the students blew up and then use tissue paper to build a “fire” inside of it.
How you get to the math …
It’s a really interesting story and fun activity but where’s the math? There are a ton of possibilities. Here is just one option: I would conclude this activity by telling the students that I know that if you measure the inside of the campfire circle, no one has a circumference (that is the name for how far it is around a circle) of more than 60 inches. I’d also make sure I had made a campfire myself of 10 inches in diameter.
Then, I’d have them measure with a tape measure and find out that I am right. I’d have everyone give me their circumference, that is, how far it is around their circle.
How do I know this? Because the circumference of a circle has a formula, that is πd = C . π is a number that is a constant. A constant means it always stays the same. It is about 3.14 . So, if I multiply 3.14 * 18 the answer is 56.52 That’s your circumference if your diameter – the distance across the circle, is 18. If it is less than 18, your circumference is less.
Does anyone want to guess the circumference of my circle with diameter of 10?
Why is this important?
Maybe you want to make pen for your sheep, horses, whatever and it is going to be a circle. Perhaps you have a contract to build a round pool, house, anything . How many feet of material do you need? Any time you know the diameter of a circle, you can compute the circumference. Maybe you are making a tipi and you want to know how big around it is going to be at the bottom so you can make a rug the exact right circumference.
I would bet you by the end of this lesson, students would know what a circumference is, what a diameter is, what π is and how to compute the circumference.
My point isn’t that STEM/ STEAM/ STREAM activities aren’t a great start but that often they are just a start and you may need to add a finish.

